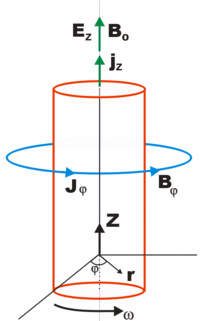
Skurcz (zwany też węzłem
lub skurczem Benneta
(nazwany tak po Willardzie Harrisonie Bennetcie), skurcz elektromagnetyczny
[1], skurcz magnetyczny
[2], efekt skurczu
[3] lub skurcz plazmy[4]) jest kompresją przewodzącego elektrycznie włókna przez siły magnetyczne. Przewodnikiem jest z reguły plazma, lecz może być to również stały lub płynny metal. W skurczu-z prąd płynie osiowo (w osi z w cylindrycznym układzie współrzędnych) a pole magnetyczne jest azymutalne. W skurczu-theta prąd jest azymutalny (w kierunku theta w cylindrycznym układzie współrz.), a pole magnetyczne jest osiowe.
Skurcze występują naturalnie w takich zjawiskach, jak pioruny[5], zorze[6], arkusze prądowe[7] i rozbłyski słoneczne[8]. Są również produkowane w laboratoriach, głównie w badaniach nad fuzją jądrową, lecz również przez hobbystów.
Wytwarzanie i rodzaje skurczów
Skurcze wytwarzane są w laboratorium na sprzęcie powiązanym z fuzją jądrową, takim, jak maszyna Z, oraz w dziedzinie fizyki wysokich energii, jak w przypadku skupiacza gęstej plazmy. Skurcze mogą się stawać niestabilne[9], oraz generować promieniowanie z całego spektrum elektromagnetycznego, włącznie z falami radiowymi, promieniowaniem rentgena[10] i gamma[11], jak również promieniowaniem synchrotronowym[12] oraz neutronami[13].
Skurczów używa się do generowania promieni rentgena, a ich silne pole magnetyczne służy w elektromagnetycznym formowaniu metali (co można zademonstrować zgniatając puszkę po napoju[14]). Mają też zastosowanie w wiązkach cząstek[15], włącznie z bronią cząsteczkową[16] oraz astrofizyką[17].
Historia

Pierwsze wytworzenie skurczu-z w laboratorium mogło mieć miejsce w 1790 w Holandii, gdy Martinus van Marum stworzył eksplozję, wyładowując 100 butelek lejdejskich do kabla.[19] Sam efekt skurczu został po raz pierwszy zaobserwowany w płynnym metalu w 1904.[20] Zjawiska tego nie rozumiano do 1905, kiedy Pollock i Barraclough[21] zbadali ściśnięty i zniekształcony przewód miedziany, w który uderzył piorun. Ich analiza wykazała, że siły wywołane oddziaływaniem przepływu dużego prądu elektrycznego, generującego własne pole magnetyczne, mogą powodować ściskanie i deformacje.[22] Podobna, i wyraźnie niezależna analiza teoretyczna, efektu skurczu w płynnych metalach opublikowana została przez Northrupp w 1907.[23] Kolejnym dużym krokiem w rozwoju była publikacja w 1934 analizy radialnego ciśnienia w statycznym skurczu-z przez Benneta[24] (zobacz następującą sekcję ze szczegółami).
Od tamtego czasu, eksperymentalny i teoretyczny postęp w nadaniach nad skurczami napędzany był badaniami nad fuzją jądrową. W swoim artykule Kablowy skurcz-z: potężne źródło promieni rentgena dla ICF
, M. G. Haines et al napisali na temat wczesnej historii badan nad skurczami-z[25]:
Ujęcie formalne
Relacja Benneta
Rozważmy cylindryczną kolumnę w pełni zjonizowanej plazmy, z osiowym polem elektrycznym, dającym osiową gęstość prądu, j, oraz towarzyszące jej azymutalne pole magnetyczne B. Gdy prąd płynie przez swoje własne pole magnetyczne, powstaje skurcz, z dośrodkową, radialną gęstością siły j x B. Jest to stały stan z równowagą sił:
- ∇p = ∇(pe + pi) = j x Β
gdzie ∇p jest gradientem ciśnienia magnetycznego a pe i pi jest odpowiednio ciśnieniem elektronów i jonów. Używając równań Maxwella ∇ x B = μ0 j oraz równania gazu doskonałego, 'p = N k T, otrzymujemy:
- <math>2 N k(T_e + T_i) = \fracSzablon:\mu 0 {4 \pi} I^2</math> (relacja Benneta)
gdzie N jest liczbą elektronów na jednostkę długości wzdłuż osi, Te oraz Ti są temperaturami elektronów i jonów, I jest całkowitym prądem wiązki a k jest stałą Boltzmanna.
Uogólniona relacja Benneta
Uogólniona relacja Benneta obejmuje skurcz plazmy przewodzącej prąd przyległy do pola magnetycznego, podlegającej obrotowi o częstotliwości kątowej ω. Wzdłuż osi cylindra plazmy prąd płynie gęstość prądu, jz, co powoduje toroidalne pole magnetyczne Βφ. Oryginalnie wyprowadzona przez Witalisa[33], uogólniona relacja Benneta wygląda następująco[34]:
- <math>\frac{1}{4} \frac{\partial^2 J_0}{\partial t^2} = W_{\perp k i n} + \Delta W_{E_z} + \Delta W_{B_z} + \Delta W_k - \fracSzablon:\mu 0 {8 \pi} I^2 (a) - \frac{1}{2}G\overline{m}^2 N^2 (a) + \frac{1}{2}\pi a^2 \epsilon_0 \left(E_r^2 (a) - E_\phi^2 (a) \right )</math>
- gdzie plazma ma promień a,
- J0 jest całkowitym momentem bezwładności względem osi,
- W⊥kin jest energią kinetyczną na jednostkę długości, ze względu na ruch poprzeczny do osi wiązki
- WBz jest energią zgodną Bz na jednostkę długości
- WEz jest energią zgodną Ez na jednostkę długości
- Wk jest energią termokinetyczną na jednostkę długości
- I(a) jest prądem osiowym wewnątrz promienia a (r na diagramie)
- N(a) jest całkowitą liczbą cząstek na jednostkę długości
- Er jest radialnym polem elektrycznym
- Eφ jest rotacyjnym polem elektrycznym
Dodatnie człony równania odpowiadają siłom ekspansyjnym, zaś ujemne oznaczają siły kompresujące wiązkę.
Relacja Carlqvista
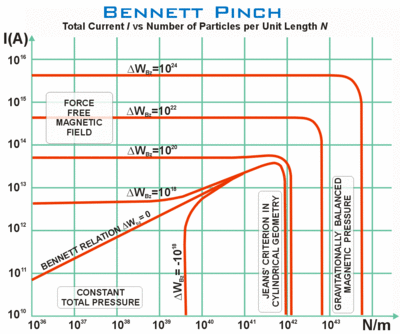
Relacja Carlqvista, opublikowana przez Charlesa Carlqvista w 1988[35], jest specjalizacją ogólnej relacji Benneta (powyżej) dla przypadku, gdy ciśnienie kinetyczne na granicy skurczu jest dużo mniejsze niż w środku. Ma ona formę
- <math>\fracSzablon:\mu 0 {8 \pi} I^2 (a) +\frac{1}{2}G\overline{m}^2 N^2 (a) = \Delta W_{B_z} + \Delta W_k</math>
i stosuje się do wielu rodzajów plazmy kosmicznej.
Relację Carlqvista można zilustrować (il. z prawej) pokazując całkowity prąd (I) w porównaniu do liczby cząstek na jednostkę długości (N) w skurczu Benneta. Wykres ilustruje cztery fizycznie odmienne regiony. Temperatura plazmy jest niska (Ti = Te = Tn = 20 K), zawierając głównie wodór, czyli cząstki o masie 3×10-27 kg. Energia termokinetyczna wynosi Wk >> π a2 pk(a). Krzywe ΔWBz pokazują różną ilość nadmiarowej energii magnetycznej na jednostkę długości, spowodowanej polem osiowym polem magnetycznym Bz. Zakłada się, że plazma nie wiruje, a ciśnienie kinetyczne na brzegach jest dużo mniejsze niż wewnątrz.
Regiony na grafice: (a) W górnym lewym obszarze dominuje siła ściskająca. (b) Idąc ku dołowi, odśrodkowe ciśnienie kinetyczne równoważy dośrodkowe ciśnienie magnetyczne, przez co całkowite ciśnienie jest stałe. (c) Z prawej strony pionowej linii ΔWBz=0, ciśnienie magnetyczne równoważy ciśnienie grawitacyjne, a siła ścisku jest zaniedbywalna. (d) Na lewo od linii opadającej ΔWBz=0, siła grawitacji jest zaniedbywalna. Pamiętajmy, że wykres przedstawia szczególny przypadek relacji Carlqvista, i jeśli zastąpić ją ogólniejszą relacją Benneta, wówczas odpowiednie regiony wykresu nie będą prawidłowe.
Carlqvist odnotował potem, że używając powyższej relacji oraz pochodnej, można opisać skurcz Benneta, kryterium Jean'a (dla grawitacyjnej niestabilności [36], w jednym i dwóch wymiarach), prądy Birkelanda, równoważone grawitacyjnie ciśnienie magnetyczne oraz ciągłe przejścia pomiędzy tymi stanami.
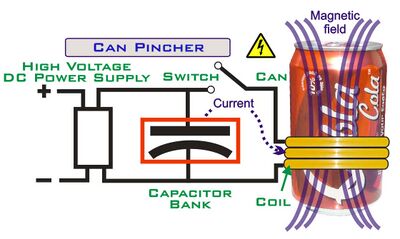
Zgniatanie puszek przy pomocy skurczu

Wielu entuzjastów wysokonapięciowej elektroniki sporządza swoje własne urządzenia wykorzystujące moc impulsową do wytwarzania skurczu theta, zdolnego zgnieść miękką puszkę aluminiową (Uwaga! Uderzenia wysokim napięciem mogą być zabójcze!).
Elektromagnetyczny zgniatacz puszek aluminiowych składa się z czterech głównych komponentów: (1) źródło prądu stałego o wysokim napięciu, będącego źródłem energii elektrycznej, (2) dużego kondensatora wyładowaniowego do akumulowania energii, (3) wysokonapięciowego przełącznika lub iskrownika oraz (4) grubej cewki, w której zostanie szybko uwolniona nagromadzona energia, aby wytworzyć odpowiednio ściskające pole magnetyczne (patrz: diagram poniżej).
W praktyce urządzenie takie jest nieco bardziej skomplikowane, gdyż w jego skład wchodzą komponenty elektryczne, regulujące przepływ prądu, w celu zmaksymalizowania efektu, oraz zabezpieczające. Więcej szczegółów znaleźć można w przypisach[37].
Zgniatacz Sama Barrosa kosztuje około $500, wykorzystuje drugi największy SCR do produkcji i 900V zestawu kondensatorów do przechowania około 3000 J energii. Na bardzo krótki czas, generuje on pole magnetyczne 250 000 razy silniejsze od ziemskiego, i moc około 22 MW.[38]
Przypisy

- ↑ Lee, S., "Energy balance and the radius of electromagnetically pinched plasma columns" (1983) Plasma Physics, Volume 25, Issue 5, pp. 571-576 (1983).
- ↑ Schmidt, Helmut, "Formation of a Magnetic Pinch in InSb and the Possibility of Population Inversion in the Pinch" (1966) Physical Review, vol. 149, Issue 2, pp. 564-573
- ↑ Severnyi, A. B., "On the Appearance of Cosmics Rays in the Pinch Effect in Solar Flares" (1959) Soviet Astronomy, Vol. 3, p.887
- ↑ Zueva, N. M.; Solov'ev, L. S.; Morozov, A. I. "Nonlinear instability of plasma pinches" (1976) Journal of Experimental and Theoretical Physics Letters, Vol. 23, p.256
- ↑ Rai, J.; Singh, A. K.; Saha, S. K, "Magnetic field within the return stroke channel of lightning" (1973) Indian Journal of Radio and Space Physics, vol. 2, Dec. 1973, p. 240-242.
- ↑ Galperin, Iu. I.; Zelenyi, L. M.; Kuznetsova, M. M. "Pinching of field-aligned currents as a possible mechanism for the formation of raylike auroral forms" (1986) Kosmicheskie Issledovaniia (ISSN 0023-4206), vol. 24, Nov.-Dec. 1986, p. 865-874. In Russian.
- ↑ Syrovatskii, S. I. "Pinch sheets and reconnection in astrophysics" (1981) In Annual review of astronomy and astrophysics. Volume 19. (A82-11551 02-90) Palo Alto, CA, Annual Reviews, Inc., 1981, p. 163-229
- ↑ Airapetyan, V. S.; Vikhrev, V. V.; Ivanov, V. V.; Rozanova, G. A. "Pinch Mechanism of Energy Release of Stellar Flares" (1990) Astrophsyics (Tr. Astrofizika) v.32 No.3 Nov. p.230 1990
- ↑ Hardee, P. E., "and pinching instability of supersonic expanding jets in extragalactic radio sources" (1982) Astrophysical Journal, Part 1, vol. 257, June 15, 1982, p. 509-526
- ↑ Pereira, N. R., et al, "[X rays from z-pinches on relativistic electron-beam generators]" (1988) Journal of Applied Physics (ISSN 0021-8979), vol. 64, Aug. 1, 1988, p. R1-R27
- ↑ Wu, Mei; Chen, Li; Li, Ti-Pei, "Polarization in Gamma-Ray Bursts Produced by Pinch Discharge" (2005) Chinese Journal of Astronomy & Astrophysics, Vol. 5, p. 57-64
- ↑ Peratt, A.L., "Synchrotron radiation from pinched particle beams", (1998) Plasma Physics: VII Lawpp 97: Proceedings of the 1997 Latin American Workshop on Plasma Physics, Edited by Pablo Martin, Julio Puerta, Pablo Martmn, with reference to Meierovich, B. E., "Electromagnetic collapse. Problems of stability, emission of radiation and evolution of a dense pinch" (1984) Physics Reports, Volume 104, Issue 5, p. 259-346.
- ↑ Anderson, Oscar A., et al, "Neutron Production in Linear Deuterium Pinches" (1958) Physical Review, vol. 110, Issue 6, pp. 1375-1387
- ↑ For example, see "Electromagnetic Crusher"
- ↑ Ryutov, D. D.; Derzon, M. S.; Matzen, M. K, "The physics of fast Z pinches" (2000) Reviews of Modern Physics, vol. 72, Issue 1, pp. 167-223
- ↑ Andre Gsponer, "Physics of high-intensity high-energy particle beam propagation in open air and outer-space plasmas" (2004) http://arxiv.org/abs/physics/0409157
- ↑ Peratt, Anthony L., "The role of particle beams and electrical currents in the plasma universe" (1988) Laser and Particle Beams (ISSN 0263-0346), vol. 6, Aug. 1988, p. 471-491.
- ↑ See also the IEEE History Center, "Evolution of the IEEE Logo" March 1963; see also the comments in "Laboratory Astrophysics"
- ↑ van Marum M 1790 Proc. 4th Int. Conf. on Dense Z-Pinches (Vancouver 1997) (Am. Inst. Phys. Woodbury, New York, 1997) Frontispiece and p ii
- ↑ Tom Dolan, "Chapter 12. Pinches and Compact Toruses" (1982) Fusion Research FULL TEXT. Uwagi: Historia badań nad fuzją w urządzeniach do skurczów jest podsumowana w: R, J. Bickerton, "Pinch Research", Nuclear Fusion 20, 1072-1075 (1980).
- ↑ Pollock J A and Barraclough S, 1905 Proc. R. Soc. New South Wales 39 131
- ↑ R. S. Pease, "The Electromagnetic Pinch: From Pollock to the Joint European Torus", "Pollock Memorial Lecture for 1984 delivered at the University of Sydney, 28 November, 1984": This review of the electromagnetic pinch starts with an exhibit taken from Pollock's work, carefully preserved and drawn to attention of modern research by Professor C. Watson-Munro. It is a compressed and distorted length of copper tube originally part of the lightning conductor on the Hartley Vale kerosene refinery in New South Wales. It was known to have been struck by lightning. Pollock and Barraclough (1905) from the Department of Mechanical Engineering at Sydney University carried out an analysis to see whether or not the compression could have arisen from the flow of electric current. They concluded that the compressive forces, due to the interaction of the large current flow with its own magnetic field could have been responsible for the compression and distortion. As far as I know, this is the first identified piece of observational data on the electromagnetic pinch; and the first theoretical discussion of the effect.
- ↑ Northrupp E F 1907 "Some Newly Observed Manifestations of Forces in the Interior of an Electric Conductor" (1907) Phys. Rev. 24 474. Napisał:
Kilka miesięcy temu, mój przyjaciel, Carl Hering, opisał mi zaskakujące i najwyraźniej nowe zjawisko, jakie zaobserwował. Odkrył on, przepuszczając względnie duży prąd zmienny przez nie elektrolityczny, płynny przewodnik, że płyn ścisnął się w przekroju i płynął w górę koryta. Mr. Hering zasugerował pomysł, że skurczenie to spowodowane bylo elastycznym działaniem linii pola magnetycznego, otaczających kołowo przewodnik... Ponieważ działanie siły na przewodnik ściska go, lub skurcza, nazwał to żartobliwie 'efektem skurczu'.
- ↑ W.H.Bennett, "Magnetically Self-Focussing Streams", Phys. Rev. 45 890 (1934)
- ↑ M G Haines, T W L Sanford and V P Smirnov, "Wire-array z-pinch: a powerful x-ray source for ICF" (2005) Plasma Phys. Control. Fusion 47 B1-B11 (online in full, click PDF).
- ↑ Thompson G P and Blackman M 1946 British Patent 817681. Haines M G 1996 "Historical Perspective: Fifty years of controlled fusion research" Plasma Phys. Control. Fusion 38 643
- ↑ Kruskal M D and Schwarzchild "Some Instabilities of a Completely Ionized Plasma" 1954 Proc. R. Soc. Lond. A 223 348
- ↑ Kurchatov I V 1957 J. Nucl. Energy 4 193
- ↑ Pease R S "Equilibrium Characteristics of a Pinched Gas Discharge Cooled by Bremsstrahlung Radiation" 1957 Proc. Phys. Soc. Lond. 70 11
- ↑ Braginskii S I 1957 Zh. Eksp. Teor. Fiz 33 645; Braginskii S I 1958 Sov. Phys.—JETP 6 494
- ↑ Haines M G et al 2005 Phys. Rev. Lett. submitted; see also EPS Conf. on Plasma Physics 2004 (London, UK) paper 73
- ↑ Curzon F L et al "Experiments on the Growth Rate of Surface Instabilities in a Linear Pinched Discharge" 1960 Proc. R. Soc. Lond. A 257 386
- ↑ Witalis, E. A. "Plasma-physical aspects of charged-particle beams" (1981) Physical Review A - General Physics, 3rd Series, vol. 24, Nov. 1981, p. 2758-2764
- ↑ Anthony L . Peratt, "Physics of the Plasma Universe", 1992 Springer-Verlag, ISBN 0-387-97575-6
- ↑ Carlqvist, Per, "Cosmic electric currents and the generalized Bennett relation" (1988) Astrophysics and Space Science (ISSN 0004-640X), vol. 144, no. 1-2, May 1988, p. 73-84
- ↑ J. H. Jeans, "The stability of a spherical nebula" Phil. Trans. R. Soc. Lond. A 199 (1902)
- ↑ Examples of electromagnetic pinch can crushers can be found at (a) Bob LaPointe's site on High Voltage Devices and Experiments (b) Tristran's Electromagnetic Can Crusher (including schematic) (c) Sam Borros's Solid State Can Crusher
- ↑ Sam Borros's PowerLabs' Solid State Can Crusher
- ↑ Trubnikov, Boris A., "A new hypothesis of cosmic ray generation in plasma pinches" (1992) IEEE Transactions on Plasma Science (ISSN 0093-3813), vol. 20, no. 6, p. 898-904.
- ↑ "The PLASMAK™ Configuration and Ball Lightning" (PDF) presented at the International Symposium on Ball Lightning; July 1988
Zobacz również
- Symetryczny torus Madisona (Skurcz o odwróconym polu, jak zrobić skurcz toroidalny)
- Maszyna Z
- Skurcz (fuzja jądrowa)