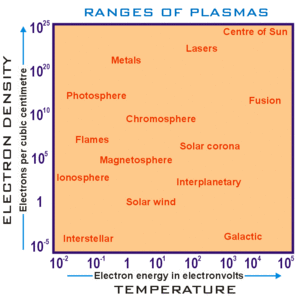
Parametry plazmy, włączając w to rozciągłość przestrzenną i czasową, mogą zmieniać się o wiele rzędów wielkości. Niemniej jednak istnieją znaczące podobieństwa pomiędzy plazmą o różnych parametrach. Zrozumienie skalowania plazmy nie jest jedynie teoretyczną ciekawostką, gdyż pozwala na odnoszenie wyników eksperymentów laboratoryjnych do naturalnej lub sztucznej plazmy w większej skali. Jest to podobne do testowania samolotów lub studiowania naturalnego przepływu powietrza w tunelu wiatrowym.
Transformacje podobieństwa (zwane także prawami podobieństwa) pomagają stwierdzić, jak właściwości plazmy zmieniają się w celu zachowania tej samej charakterystyki. Pierwszym potrzebnym krokiem jest wyrażenie praw rządzących układem w sposób bezwymiarowy. Wybór parametrów bezwymiarowych nie jest unikalny i jest to zwykle możliwe jedynie poprzez zignorowanie pewnych aspektów układu.
Jednym z bezwymiarowych parametrów plazmy jest stosunek masy jonów do elektronów. Ponieważ z reguły jest on duży, wynosząc przynajmniej 1836, w teoretycznej analizie często przyjmuje się go za nieskończony, czyli elektrony uważa się za bezmasowe, albo jony za nieskończeni ciężkie. W badaniach numerycznych często pojawia się odwrotny problem. Jeśli używa się realistycznego stosunku, czas obliczeń jest duży, dlatego stosuje się mniejsze, ale wciąż duże wartości, np. 100. Do analizy pewnych zjawisk, takich jak niższe oscylacje hybrydowe, należy używać właściwej wartości.
Powszechnie stosowane transformacje podobieństwa
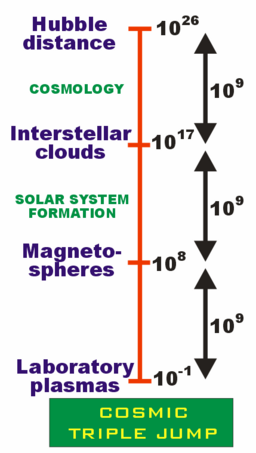
Jedną z powszechnie używanych transformacji jest ta otrzymana dla wyładowań w gazach przez Jamesa Dillona Cobine'a (1941)[3], Alfreda Hansa von Engela i Maxa Steenbecka (1934)[4], zastosowana później przez Hannesa Alfvéna i Carla-Gunne'a Fälthammara do plazmy.[5] Można je podsumować następująco:
Transformacje podobieństwa zastosowane do wyładowań w gazach i niektórych rodzajów plazmy
| Property | Czynnik skali | |
|---|---|---|
| długość, czas, induktancja, pojemność | x1 | x |
| energia cząstki, prędkość, potencjał, prąd, opór | x0=1 | niezmieniony |
| pola magnetyczne i elektryczne, przewodność, gęstość gazu obojętnego, stopień jonizacji | x-1 | 1/x |
| gęstość prądu, gęstości jonów i elektronów | x-2 | 1/x2 |
Skalowanie najlepiej pasuje do plazmy o względnie niskim stopniu jonizacji. W plazmie takiej energia jonizacji obojętnych atomów jest istotnym parametrem i ustanawia absolutną skalę energii, wyjaśniającą wiele z przeskalowań z tabeli:
- Ponieważ masy elektronów i protonów są niezmienne, prędkości cząstek również są stałe, jak prędkość dźwięku.
- Jeżeli prędkości są stałe, wówczas skala czasu musi być wprost proporcjonalna do skali odległości.
- W przypadku, gdy naładowane cząstki, opadające wraz z potencjałem, mają tą samą energię, potencjały muszą być niezmiennikiem, implikując, że pole elektryczne skaluje się odwrotnie do odległości.
- Przyjmując, że dryf E-przez-B jest istotny i powinien być niezmiennikiem, pole magnetyczne musi się skalować jak elektryczne, czyli odwrotnie do rozmiaru. Skalowanie to wymagane jest również przez prawo Faradaya i Ampère'a.
- Przyjmując, że prędkość fali Alfvéna jest istotna i musi być niezmiennicza, gęstość jonów (wraz z gęstością elektronów) musi skalować się wraz z 2, czyli odwrotnie do kwadratu rozmiarów. Zakładając, że temperatura jest stała, zapewnia to również stały stosunek energii termicznej do magnetycznej, znany jako beta. Co więcej, w regionach, gdzie nie jest to spełnione, skalowanie to wymagane jest przez prawo Gaussa.
- Prawo Ampère'a wymaga również, aby gęstość prądu skalowała się odwrotnie do kwadratu rozmiarów, a zatem sam prąd jest niezmiennikiem.
- Przewodność elektryczna jest gęstością prądu podzieloną przez pole elektryczne, a tym samym skaluje się odwrotnie proporcjonalnie do długości.
- W częściowo zjonizowanej plazmie przewodność elektryczna jest proporcjonalna do gęstości elektronów a odwrotnie proporcjonalna do gęstości obojętnego gazu, przez co gęstość obojętna musi skalować się odwrotnie do odległości, podobnie jak stopień jonizacji.
Ograniczenia
Chociaż przekształcenia podobieństw zachowują część podstawowych własności plazmy, nie wszystkie zjawiska plazmowe się skalują w ten sposób. Załóżmy, na przykład, stopień jonizacji, który jest bezwymiarowy, i powinien pozostać idealnie niezmieniony przy skalowaniu układu. Liczba naładowanych cząstek na jednostkę objętości jest proporcjonalna do gęstości prądu, która skaluje się jak x-2, podczas, gdy liczba cząstek obojętnych skaluje się jak x-1, zatem stopień jonizacji również skaluje się jak x-1.
Zastosowania astrofizyczne
Jako przykład można wziąć pasmo zorzy polarnej, o grubości ok 1 km. W symulacji laboratoryjnej może ono mieć 10 cm grubości, czyli mniej o 104. Aby spełnić warunki transformacji podobieństwa, gęstość gazowa musi się zwiększyć o taki sam czynnik, z 104 m-3 do 108 m-3 1010 cm-3 do 104 cm-3), a pole magnetyczne musi wzrosnąć o ten sam czynnik, z 50 mikrotesli do 500 militesli (0,5 gaussa do 5 kilogausów). Wartości te są duże, lecz w zasięgu technologii. Jeżeli eksperyment uchwyci typowe zachowanie zorzy, to proces ten będzie przebiegał 104 razy szybciej, zatem puls, który w przyrodzie zajmie 100s, w laboratorium potrwa tylko 10 ms.
Transformacje podobieństwa zastosowane do niektórych rodzajów plazmy astrofizycznej
Prawdziwe własności plazmy w porównaniu plazmy laoratoryjnej, gdy skalę zredukuje się do 10 cm.
| Region | Wymiar charakterystyczny (cm) | Gęstość (cząstki/cm3) | Pole magnetyczne (w gaussach) | Czas charakterystyczny | |||||
| Właściwy | Skalowany | Czynnik skali | Właściwy | Skalowany | Właściwy | Skalowany | Właściwy | Skalowany | |
| Jonosfera | 106 - 107 | 10 | 10-5 - 10-6 | 1010 | 1015 - 1016 | 0.5 | 5x104 - 5x105 | Okres Wielkiej Pulsacji | |
| 100 s | 0.1 - 1 ms | ||||||||
| Egzosfera | 109 | 10 | 10-8 | 105 - 10 | 1013 - 109 | 0.5 - 5x10-4 | 5x107 - 5x104 | Jeden dzień | |
| 105 s | 1 ms | ||||||||
| Przestrzeń międzyplanetarna | 1013 | 10 | 10-12 | 1 - 10 | 1012 - 1013 | 10-4 | 108 | Jeden obrót słoneczny | |
| 2x106 s | 2 μs | ||||||||
| Przestrzeń międzygwiezdna | 3x1022 | 10 | 3x10-22 | 1 | 3x1021 | 10-6 - 10-5 | 3x1015 - 3x1016 | Okres obrotu galaktycznego | |
| 1x1016 s | 3 μs | ||||||||
| Przestrzeń międzygalaktyczna | >3x1027 | 10 | <3x10-27 | 10-4? | >3x1022 | 10-7? | >3x1019 | Wiek Wszechświata | |
| 4x1017s | 1x10-9s | ||||||||
| Słoneczna chromosfera | 108 | 10 | 10-7 | 1011 - 1014 | 1018 - 1021 | 103 - 1 | 1010 - 107 | Czas życia rozbłysku słonecznego | |
| 103 s | 100 μs | ||||||||
| Czas życia rozbłysku słonecznego | |||||||||
| 105 s | 10 ms | ||||||||
| Korona słoneczna | 1010 - 1011 | 10 | 10-9 - 10-10 | 108 - 106 | 1017 - 1016 | 102 - 10-1 | 1011 - 109 | Czas życia łuku koronalnego | |
| 103 s | 10-1 to 1 µs | ||||||||
| Cykl słoneczny | |||||||||
| 22 lata | 70 do 700 ms | ||||||||
Gęstość cząstek atmosfery ziemskiej na poziomie morza wynosi 1019 na cm3
Mały magnes sztakowy = 100 millitesli. Duży elektromagnes = 2 tesli
109 cm = 10,000 km
Tabela pokazuje właśności niektórych rodzajów plazmy kosmicznej (kolumna o nazwie Właściwy
). Pokazuje również, jak inne właśności plamzy muszą się zmienić, jeżeli (a) długość charakterystyczna zmniejszy się do 10 cm, oraz (b) charakterystyka plazmy pozostanie niezmieniona.
Po pierwsze należy wspomnieć, że wiele zjawisk kosmicznych jest nie od odtworzenia w laboratorium, gdyż potrzebne natężenie pola magnetycznego jest poza możliwościami technologii. Spośród wymienionych w tabeli, tylko jonosfera oraz egzosfera mogą być przeskalowane do laboratorium. Kolejnym problemem jest stopień jonizacji. Przy przeskalowaniu rozmiarów o wiele rzędów wielkości, założenie o częściowym zjonizowaniu może nie być spełnione w symulacji. Końcowe obserwacje są takie, że gęstości plazmy potrzebne w laboratorium sięgają 1016 cm-3 dla jonosfery, w porównaniu z ciśnieniem atmosferycznym 1019 cm-3. Innymi słowy, laboratoryjna analogia rozrzedzonej plazmy kosmicznej to już nie komora próżniowa
, lecz plazma pod ciśnieniem, gdzie wchodzą w grę wyższe temperatury, a ciśnienie sięga atmosferycznego.
Przypisy
- ↑ After Peratt, A. L., "Advances in Numerical Modeling of Astrophysical and Space Plasmas" (1996) Astrophysics and Space Science, v. 242, Issue 1/2, p. 93-163. FULL TEXT PEERREVIEWED
- ↑ Hannes Alfvén, "On hierarchical cosmology" FULL TEXT (1983) Astrophysics and Space Science (ISSN 0004-640X), vol. 89, no. 2, Jan. 1983, p. 313-324. PEERREVIEWED
- ↑ Cobine, J. D ., 1941: Gaseous Conductors, McGraw-Hill . New York. ACADEMIC BOOK
- ↑ von Engel, A., and Steenbeck, M., 1934: ElektrischeGasentladungen, Springer-Verlag, Berlin. See also von Engel, 1955: Ionized Gases, Clarendon Press, Oxford.
- ↑ H. Alfvén and C.-G. Falthammar, Cosmic electrodynamics (2nd Edition, Clarendon press, Oxford, 1963) See 4.2.2. Similarity Transformations. ACADEMIC BOOK
Bibliografia
- Peratt, A. L., "Advances in Numerical Modeling of Astrophysical and Space Plasmas" (1996) Astrophysics and Space Science, v. 242, Issue 1/2, p. 93-163. FULL TEXT PEERREVIEWED
- Peratt, Anthony L., "Advances in Numerical Modeling of Astrophysical and Space Plasmas", Astrophysics and Space Science, v. 256, Issue 1/2, p. 51-75 (1997) Paper FULL TEXT PDF PEERREVIEWED